NumPy

NumPy, short for Numerical Python, is an open-source Python library that specializes in numerical computing. It is a fundamental package for scientific computing in Python, providing support for arrays, matrices, and a suite of mathematical functions to operate on these data structures. NumPy is the backbone of many data science and machine learning workflows, offering the computational power of languages like C and Fortran while maintaining Python’s simplicity and ease of use. The library is particularly valued for its ability to allow researchers and developers to perform complex mathematical operations on large datasets efficiently, making it a cornerstone in fields that require extensive data analysis and manipulation.

Core Concepts

NumPy Arrays

At the heart of NumPy is the ndarray (N-dimensional array) object, which is a powerful data structure for efficient storage and manipulation of homogeneous data types. Unlike Python lists, NumPy arrays are optimized for operations on large datasets, making them significantly faster and more efficient. The ndarray supports a variety of operations, such as element-wise arithmetic, statistical computations, and data reshaping, all while ensuring consistent performance across operations.

• Fixed Size: Once created, the size of a NumPy array is fixed. If you need to change the size, a new array must be created. This immutability allows NumPy to optimize memory usage and processing speed.
• Data Type Homogeneity: All elements in a NumPy array must be of the same data type, ensuring uniformity in operations. This homogeneity is what enables NumPy to perform vectorized operations efficiently.
• Efficient Operations: NumPy arrays support a vast range of mathematical operations that are implemented in pre-compiled C code, enhancing performance. This includes operations like addition, subtraction, and multiplication that are executed at a fraction of the time it would take using native Python structures.

Multidimensional Arrays

NumPy excels in handling multidimensional arrays, which are essential for various scientific computations. These arrays can represent vectors (1-D), matrices (2-D), or tensors (N-D), enabling complex data manipulation with ease. The ability to handle multidimensional arrays effectively makes NumPy a preferred choice for applications in machine learning and scientific computing, where data often comes in multi-tiered structures.

Vectorization and Broadcasting

One of NumPy’s key strengths is its ability to perform vectorized operations, meaning operations that apply to entire arrays rather than individual elements. This approach is not only more concise but also faster due to underlying C implementations. Vectorization significantly reduces the overhead of executing loops in Python, leading to more performant code. Broadcasting extends this capability by allowing operations on arrays of different shapes, aligning them to a common shape in an efficient manner. This feature simplifies code and reduces the need for complex looping constructs.

Features and Functionality

Mathematical Functions

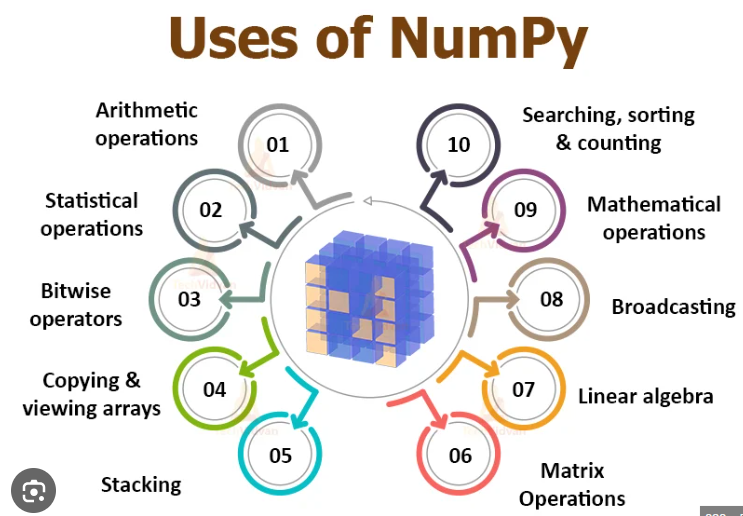
NumPy includes numerous functions to perform operations such as:

• Linear Algebra: Functions for matrix operations, eigenvalues, and other linear algebraic computations. These functions are crucial for solving systems of equations and performing matrix decompositions, which are common in scientific computing.
• Fourier Transforms: Capabilities for computing fast Fourier transforms. FFTs are used in signal processing and other fields that require frequency analysis.
• Random Number Generation: Tools for generating random numbers and performing random sampling. This is essential for simulations and stochastic modeling.
• Statistical Operations: Functions to compute statistics like mean, median, and standard deviation. These operations are foundational in data analysis and help in understanding data distributions.

Integration with Other Libraries

NumPy is foundational to the scientific Python ecosystem, serving as the base for libraries like Pandas, SciPy, and Scikit-learn. These libraries rely on NumPy’s array structures for efficient data manipulation and analysis. For instance, Pandas uses NumPy’s arrays for its DataFrame objects, while SciPy builds on NumPy for more advanced mathematical functions, and Scikit-learn uses them for efficient machine learning algorithms.

GPU Acceleration

While NumPy is optimized for CPU operations, libraries like CuPy and frameworks like PyTorch extend NumPy’s capabilities to GPUs, leveraging parallel processing for faster computation in machine learning and data science applications. This allows users to harness the power of GPUs to accelerate computationally intensive tasks without having to learn a completely new library.

Use Cases

Scientific Computing

NumPy is indispensable in fields like physics, chemistry, and biology, where it facilitates simulations, data analysis, and model building. Researchers use NumPy to handle large datasets and perform complex mathematical computations efficiently. Its ability to seamlessly integrate with other scientific libraries makes it a versatile tool for developing comprehensive computational models.

Data Science and Machine Learning

In data science, NumPy is used for data preprocessing, feature extraction, and model evaluation. Its array operations are crucial for handling large datasets, making it a staple in machine learning workflows. NumPy’s fast and efficient operations allow data scientists to prototype quickly and scale up their solutions as needed.

AI and Automation

NumPy’s role in AI and automation is significant, offering the computational backbone for deep learning frameworks like TensorFlow and PyTorch. These frameworks use NumPy for tensor manipulation and numerical computation, essential for training and deploying AI models. The ability to handle large amounts of data efficiently makes NumPy a key component in developing AI-driven solutions.

Examples and Code Snippets

Creating and Manipulating Arrays

import numpy as np

# Creating a 1-D array
array_1d = np.array([1, 2, 3, 4, 5])

# Creating a 2-D array (matrix)
array_2d = np.array([[1, 2, 3], [4, 5, 6]])

# Accessing elements
element = array_1d[0]  # Outputs 1

# Reshaping arrays
reshaped_array = array_2d.reshape(3, 2)

# Arithmetic operations
result = array_1d * 2  # Outputs array([2, 4, 6, 8, 10])

Broadcasting Example

# Broadcasting a scalar value across a 1-D array
array = np.array([1, 2, 3])
broadcasted_result = array + 5  # Outputs array([6, 7, 8])

# Broadcasting with different shapes
array_a = np.array([[1], [2], [3]])
array_b = np.array([4, 5, 6])
broadcasted_sum = array_a + array_b
# Outputs array([[5, 6, 7],
#                [6, 7, 8],
#                [7, 8, 9]])

Understanding NumPy: A Key Library in Scientific Computing

NumPy is a fundamental library in the Python programming language, widely used for numerical computations. It provides a powerful array object, and is a key component for efficient scientific computation.

1. In the paper “The NumPy array: a structure for efficient numerical computation” by Stefan Van Der Walt, S. Chris Colbert, and Gaël Varoquaux, the authors explain how NumPy arrays have become the standard for numerical data representation in Python. They discuss techniques such as vectorizing calculations, minimizing data copying, and reducing operation counts to enhance performance. The paper delves into the structure of NumPy arrays and illustrates their application in efficient computing. Read more
2. Claas Abert and colleagues, in their work “A full-fledged micromagnetic code in less than 70 lines of NumPy,” demonstrate the power of NumPy by developing a complete micromagnetic finite-difference code using the library. This code efficiently computes exchange and demagnetization fields using NumPy’s array structures, emphasizing its utility in algorithm development. Read more
3. The paper “A Toolbox for Fast Interval Arithmetic in numpy with an Application to Formal Verification of Neural Network Controlled Systems” by Akash Harapanahalli, Saber Jafarpour, and Samuel Coogan introduces a toolbox for interval analysis using NumPy. This toolbox facilitates formal verification of systems controlled by neural networks by efficiently computing natural inclusion functions within NumPy’s framework. Read more